Grounding Design Calculations – Part One ~ Electrical Knowhow

We mean by domestic, commercial and industrial premises, all installations up to 1,000 V ac and 1,500 V dc - between phases, with some minor exceptions.

1- Standards

Standards used for ground calculations of Domestic, commercial and industrial premises are:

BS 7671: Requirements for Electrical Installations. (This is also known as the IEE Wiring Regulations),
BS 7430:2011 Code of practice for protective earthing of electrical installations,
IEEE 142: Recommended Practice for Grounding of Industrial and Commercial Power Systems,
NFPA 70: National Electrical Code (NEC), Article 250.

2- What do we need to calculate?

There are many parameters to be calculated when designing grounding systems for Domestic, commercial and industrial premises as follows:

Earth/grounding electrode resistance,
Grounding conductor resistance,
Grounding electrode conductor size,
Equipment ground conductor (EGC) size.

Notes:

Step and touch voltage are not an issue in low voltage installations, since the maximum phase to earth voltage is 230 V. But you must note that some industrial installations have high fault current levels and hence, the step and touch voltages need to be calculated.

For Domestic, commercial and industrial premises, Grounding electrodes are usually sufficient to meet the basic requirements of a well-designed grounding system. But for High and medium voltage electricity substations, a common design is to lay a mesh of grid with vertical and horizontal conductors.

3- Methods of Grounding Design Calculations

There are many methods can be used for performing Grounding System Design Calculations But the common methods are:

Equations Method,
Nomographs Method,
Excel Spreadsheets Method,
Tables Method,
Online Earthing Calculators Method,
Software Programs Method.

First: Equations Method

1- Prerequisites

The following information is required / desirable before starting the calculation:

A layout of the site,
Maximum earth fault current into the earthing grid,
Maximum fault clearing time,
Ambient (or soil) temperature at the site,
Soil resistivity measurements at the site (for touch and step only),
Resistivity of any surface layers intended to be laid (for touch and step only).

2- Earth/grounding electrode resistance Calculations

Sometimes it called “Resistance to Earth calculations” and can be obtained either by using BS or IEEE standards rules as it will be explained in below.

First: Using IEEE 142 Standard

By using IEEE 142: Recommended Practice for Grounding of Industrial and Commercial Power Systems, The resistance to earth can be calculated by the formulas presented in Table-1.

Table-1

Second: Using BS 7430 Standard

The most common types of electrodes included in BS 7430 are as follows:

Vertical Rods,
horizontal strip electrode (circular or rectangular section),
Plates electrodes,
reinforced concrete foundation footings,
electrode surronded by an infill of materials,
Three rods at the vertices of an equilateral triangle,
Two strips set at right angles to each other meeting at one corner,
Three strips set at 120° meeting at the star point all of equal length,
Four strips set in a cruciform.

2.1 Vertical Rods

The resistance to earth of a vertical rod electrode is given by the following equations:

a- In Metric Units:

Where:

R is the resistance to earth in ohms,

ρ is the resistivity of the soil, in Ω-m,

L is the length of electrode, in meters,

D is the diameter of the rod in meters.

b- in English Units:

Where:

R is the resistance to earth in ohms,

ρ is the resistivity of the soil, in Ω-m,

L is the length of electrode, in feets,

D is the diameter of the rod in inches.

Example#1:

For a vertical rod electrode having 20mm diameter and 3 m length, calculate the resistance to earth noting that soil resistivity is 50 Ω-m.

Solution:

The resistance to earth of a vertical rod electrode is given by the following equation:

R= ρ * { loge (8L / d) -1 } / 2ΠL = 50 * { log_e (8*3 / 0.02) -1 } /2*3.14*3 = 16.1 ohm

Example#2:

For a vertical rod electrode having 25mm diameter and 2 m length, calculate the resistance to earth noting that soil resistivity is 30 Ω-m.

Solution:

The resistance to earth of a vertical rod electrode (R) in ohms is given by the following equation:

R= ρ * { loge (8L / d) -1 } / 2ΠL = 30 * { log_e (8*2 / 0.025) -1 } /2*3.14*2 = 13.0 ohm

2.2 Parallel connection of aligned rods

Multiple electrodes in parallel yield lower resistance to ground than a single electrode. Multiple rods are commonly used to provide the low grounding resistance required by high-capacity installations. Adding a second rod does not, however, provide a total resistance of half that of a single rod, unless the two are several rod lengths apart.

a- From BS 7430:

The resistance Rt in ohms (Ω) of n vertically driven rods set s metres apart may be calculated from:

where:

ρ is the resistivity of soil, in ohm metres (Ωm);

L is the length of the electrode, in metres (m);

n is the number of rods;

s is the spacing between the rods, in metres (m).

b- as per IEEE 142:

A useful rule is that grounding systems of 2–24 rods placed one rod length apart in a line, hollow triangle, circle, or square will provide a grounding resistance divided by the number of rods and multiplied by the factor F taken from Table-2.

Table-2

Notes:

Additional considerations with respect to step and touch potentials would be addressed by the geometry.

Placing additional rods within the periphery of a square, circle, or other shape will not appreciably reduce the grounding.

2.3 For horizontal strip electrode (circular or rectangular section)

The resistance Rta in ohms (Ω) of a strip or round conductor may be calculated from:

Where:

Rta = Resistance in ohms,

ρ is the resistivity of soil, in ohm metres (Ωm);

L is the length of the strip or conductor, in metres (m);

h is the depth of the electrode, in metres (m);

d is the diameter of the round conductor or diameter of the equivalent cross sectional area of the strip, in metres (m).

Note:

This equation is for a straight run of conductor only.

Paralleling of Strips

When two or more strips in straight lengths, each of length L in metres (m) and a separation distance s metres are laid parallel to each other and connected together at one end only the combined resistance may be calculated from the following equation:

Rn = FR1

Where:

Rn is the resistance of n conductors in parallel, in ohms (Ω)

R1 is the resistance of a single strip of length L, calculated from the preceding Rta equation, in ohms (Ω).

F has the following value:

For two lengths, F = 0.5 + [0.078(s/L)]−0.307

For three lengths, F = 0.33 + [0.071(s/L)]−0.408

For four lengths, F = 0.25 + [0.067(s/L)]−0.451

Provided that 0.02 < (s/L) < 0.3.

2.4 For Plates electrodes

The resistance to earth of a plate electrode is given by the following equation:

Where:

R = Resistance in ohms,

ρ = Soil resistivity in ohm metres (Ω-m),

A = The Area of one face of the plate, in m².

Notes:

Plates, if used, should be installed as small units of not greater than 1.2 m × 1.2 m connected in parallel vertically and at least 2 m apart.

The minimum ground cover should not be less than 600 mm and ideally the surrounding soil should be damp.

Connections to the plate should be by copper conductor, welded, riveted or otherwise attached with material that will not cause corrosion at the joint.

The finished joint should be covered with a heavy coat of bitumen.

The connecting strip to the above ground disconnection point should be fully insulated to avoid electrolytic action.

Where the plate is placed in a cut out slot, e.g. in a chalk bed near the surface, the slot should be big enough to allow at least 300 mm thickness of soil or other conducting low resistivity medium cover around the whole plate. This requires careful assembly during installation to ensure that the bottom of the plate is resting in the medium used and not on the chalk or high resistivity substrata.

2.5 For structure steelwork

Foundation metalwork in concrete may be used as a ready made and effective earth electrode. The total electrode area formed by the underground metalwork of large structure may often be used to provide an earth resistance lower then that obtainable by other methods; overall values well below 1 Ω are obtainable.

The resistance to earth of a reinforced concrete foundation can be estimated by assuming the following:

Only the vertical reinforcing rods are bonded to the building structure or to the earthing system and the effect of other reinforcement is neglected.

The reinforced rods are equally spaced in symmetrical pattern.

So, the resistance to earth of a reinforced concrete foundation will be given by the following equation:

Where:

R = Resistance in ohms,

ρ = Soil resistivity in ohm metres (Ω-m),

ρ_c = Concrete resistivity in ohm metres (Ω-m),

L = Length of reinforcing rod below ground level in metres,

δ= thickness of concrete between rods and soil in meters,

Z = geometric mean distance of rod cluster in meters from Table-3,

Table-3

The combined effect of all similar footings Rtot in ohms (Ω), assumed to be arranged in an approximately rectangular plan, may be determined from the following:

Where:

R1 is the resistance of one footing, in ohms (Ω);

λ is the factor from Table 4;

ρ is the resistivity of soil, in ohm metres (Ωm);

s is the spacing of footings, in metres (m);

n is the number of footings used as electrodes (see the note to Table 4).

Note:

This equation is based on the assumption that the spacing between adjacent electrodes is such that the ratio ρ/2πR1s is less than approximately 0.2.

Table 4

Notes:

It is important that consideration is given to the possibility of corrosion of the metalwork reinforcement; It might be necessary to consider the need for cathodic protection.

Wherever significant continuous earth leakage current is expected, it is recommended that a main electrode of the types of earth electrodes be provided to which the foundation electrodes can be bonded to provide auxiliary electrodes, thus giving assistance to high fault currents.

Corrosion of concrete encased steelwork, subject to a.c. fault currents within its carrying capability, may be assumed to be negligible.

The resistance to earth of concrete encased steelwork or of concrete reinforcing bars varies according to the type of soil, its moisture content, and the design of the foundation. Concrete is hygroscopic and, except in dry locations, when buried in soil, it may be expected to have a resistivity of about 30 Ωm to 90 Ωm, at normal temperatures; this is lower than some types of soil.

It is essential to measure the resistance to earth of any metalwork it is intended to use as an electrode, and to monitor its value at regular intervals afterwards, in order to confirm that it continues to provide an adequate connection to earth.

The large proportion of the resistance is due to the concrete to earth is immediately around the metalwork and is dependent on its moisture content. After construction and with the passage of time this moisture content will approach equilibrium with that of the soil, and will usually be dryer than when first laid.

Allowance should be made for the consequent increase in electrode resistance due to changes in moisture content when using measurements made during the installation of a structure.

It is important to ensure electrical continuity between all metalwork considered to be part of the electrode. In the case of contacts between metalwork within concrete or below ground, such as reinforcing bars, this may best be effected by welding; above ground and at anchor bolts it may generally done by attaching a bond conductor to bypass each structural joint. This applies particularly to surfaces which might have been primed before assembly.

2-6 resistance of an electrode surrounded by an infill of materials (such as bentonite or concrete)

In this case, The following equation will be used:

Where:

ρ Is the resistivity of soil in ohm metres (Ω-m),

ρ_c Is the resistivity of infill material in ohm metres (Ω-m),

d is the diammeter of electrode in meter,

L is the driven length of electrode in meter.

Note:

Generally the above equation will be used when the electrode is encased in low resistivity material

2.7 Three rods at the vertices of an equilateral triangle

The resistance Re in ohms (Ω) of three interconnected rods set out at the vertices of an equilateral triangle [see Figure 1-a ] of side s metres length may be calculated from:

Figure 1

The resistance of various constructions of horizontally placed simple earthing electrodes can be calculated using the following equation:

Where:

ρ is the resistivity of soil, in ohm metres (Ωm);

L is the length of rod, in metres (m);

d is the diameter of rod, in metres (m);

s is the length of one side of the equilateral triangle, in metres (m).

2.8 Two strips set at right angles to each other meeting at one corner

The resistance RL in ohms (Ω) of two strips of equal length set at 90° with one corner touching [see Figure 1-b ] may be calculated from:

Where:

ρ is the resistivity of soil, in ohm metres (Ωm);

L is the total length of strip in metres (m);

h is the depth of burial in metres (m);

d is the diameter of the round conductor or diameter of the equivalent cross sectional area of the strip in metres (m)

2.9 Three strips set at 120° meeting at the star point all of equal length

The resistance RS in ohms (Ω) of a star arranged strip [see Figure 1-c ] may be calculated from:

Where:

ρ is the resistivity of soil, in ohm metres (Ωm);

L is the total length of strip in metres (m);

h is the depth of burial in metres (m);

d is the diameter of the round conductor or diameter of the equivalent cross sectional area of the strip in metres (m).

2.10 Four strips set in a cruciform

The resistance Rcr in ohms (Ω) of four strips set out in a cruciform [see Figure 1-d] may be calculated from:

Where:

ρ is the resistivity of soil, in ohm metres (Ωm);

L is the total length of strip in metres (m);

h is the depth of burial in metres (m);

d is the diameter of the round conductor or diameter of the equivalent cross sectional area of the strip in metres (m).

Now, We finish the first method of grounding design calculations: Equations Method, the other methods of grounding design calculations are summarized in the below table.

Methods of Grounding Design Calculations

There are many methods can be used for performing Grounding System Design Calculations But the common methods are:

Equations Method,
Nomographs Method,
Excel Spreadsheets Method,
Tables Method,
Online Earthing Calculators Method,
Software Programs Method.

In the next Article, I will explain Other Methods of Grounding Design Calculations. Please, keep following.

Back To Course EE-5: Grounding System Design Calculations

3 comments:

moazAugust 1, 2015 at 1:39 PM
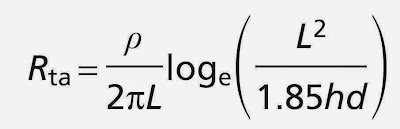
excuse me in this" part:2.7 Three rods at the vertices of an equilateral triangle" where is the soil resistivity in the equation
Kaisar DarainMay 14, 2018 at 11:31 AM
Nice to read it
AnonymousMay 5, 2022 at 7:18 AM
hi may I know where to find the source of equations for k1 and k2? Just want to verify the source so that we can proceed to indicate it. Thanks a lot!

Grounding Design Calculations – Part One

3 comments:

Translate

Contact Form